[Lab ACSD] 5. Análisis de la respuesta en frecuencia

Planteamiento del problema

8.24 Considere el sistema definido mediante:

Hay cuatro diagramas de Nyquist individuales implícitos en este sistema. Dibuje dos diagramas de Nyquist individuales para la entrada U1 en un gráfico y dos diagramas de Nyquist para la entrada U2 en otro gráfico.
Utilice MATLAB para obtener éstos dos gŕaficos.

Solución

La solución a este problema la planteare en OCTAVE,  lo dividiré en 2 partes:

• Hallar las funciones de transferencia
• Dibujar los diagramas de Nyquist

Primero, necesitamos cargar los datos del sistema en OCTAVE de la siguiente manera:

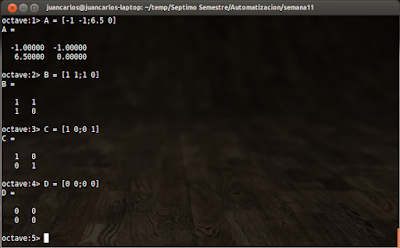
octave:1> A = [-1 -1;6.5 0];
octave:2> B = [1 1;1 0];
octave:3> C = [1 0;0 1];
octave:4> D = [0 0;0 0];

Ejecución:

Como ya hemos notado, el sistema se encuentra representado en la forma canónica, entonces hay que convertirlo a forma algebraica para poder utilizar la función nyquist en OCTAVE, eso se logra con el comando:

octave:5> pkg load signal
octave:6> [num, den] = ss2tf(A,B,C,D,1)

El comando anterior nos regresa 2 arreglos, uno con los 4 numeradores y otro con los 4 denominadores, correspondientes (por pares) a las 4 funciones de transferencia, y por consiguiente, a los 4 diagramas de Nyquist.

Ejecución:

Ahora vamos a formar las 4 funciones de transferencia con los siguientes comandos, utlizando los correspondientes numeradores y denominadores por pares:

octave:7> sys1 = tf(num{1}, den{1});
octave:8> sys2 = tf(num{2}, den{2});
octave:9> sys3 = tf(num{3}, den{3});
octave:10> sys4 = tf(num{4}, den{4});

Ejecución:

Con esto queda concluida la parte de obtener las funciones de transferencia.

Ahora vamos a dibujar los diagramas de Nyquist tal como lo especifica, para ello utilizamos los siguientes comandos:

octave:11> nyquist(sys1);
octave:12> hold on;
octave:13> nyquist(sys2);

Lo que da como resultado el primer diagrama para la entrada U₁(sys1 es el diagrama ovalado pequeño y sys2 el diagrama externo)

Despues liberamos

octave:14> hold off;

Y dibujamos el segundo par

octave:15> nyquist(sys3);
octave:16> hold on;
octave:17> nyquist(sys4);

Lo que da como resultado el diagrama para la entrada U₂ (sys3 es el diagrama ovalado pequeño y sys4 el diagrama externo)

Ejecución de los 2 pasos anteriores:

Asi concluye la actividad, espero les sirva como buena referencia. Saludos.

Referencias:

• http://elisa.dyndns-web.com/~elisa/teaching/sys/control/frecuencia.pdf
• http://elisa.dyndns-web.com/~elisa/teaching/sys/control/estados.pdf